First Principle (definition) of Differentiation
Please
look carefully the following operations in order to get a comprehensive
understanding of principle of differentiation:
WE ARE FINDING THE INSTANTANEOUS SLOPE AT A PARTICULAR POINT ON
THE GRAPH.
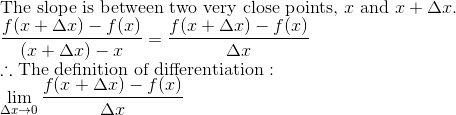
Can’t get it? Let’s look
at some typical examples.
You need to have basic ideas
of binomial theorem for this example. If you are not sure, click Binomial Theorem.
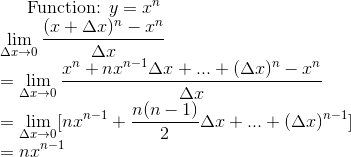
For one more example: this
time y=ln x
You also need some
background knowledge about the number e. Click
here.
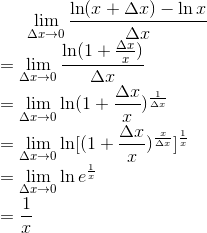
This is why e is so intriguing
to mathematicians with the logarithm of its base having this fascinating derivative.
Sometimes for other
functions, it may not be easy to differentiate with direct methods.
Some common rules (proof
omitted):
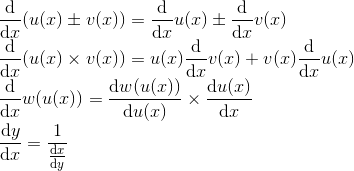
These are, respectively,
called sum, product, chain and reciprocal rules.
The next page is a list of
formulae convenient for any finding of the derivatives without proof.