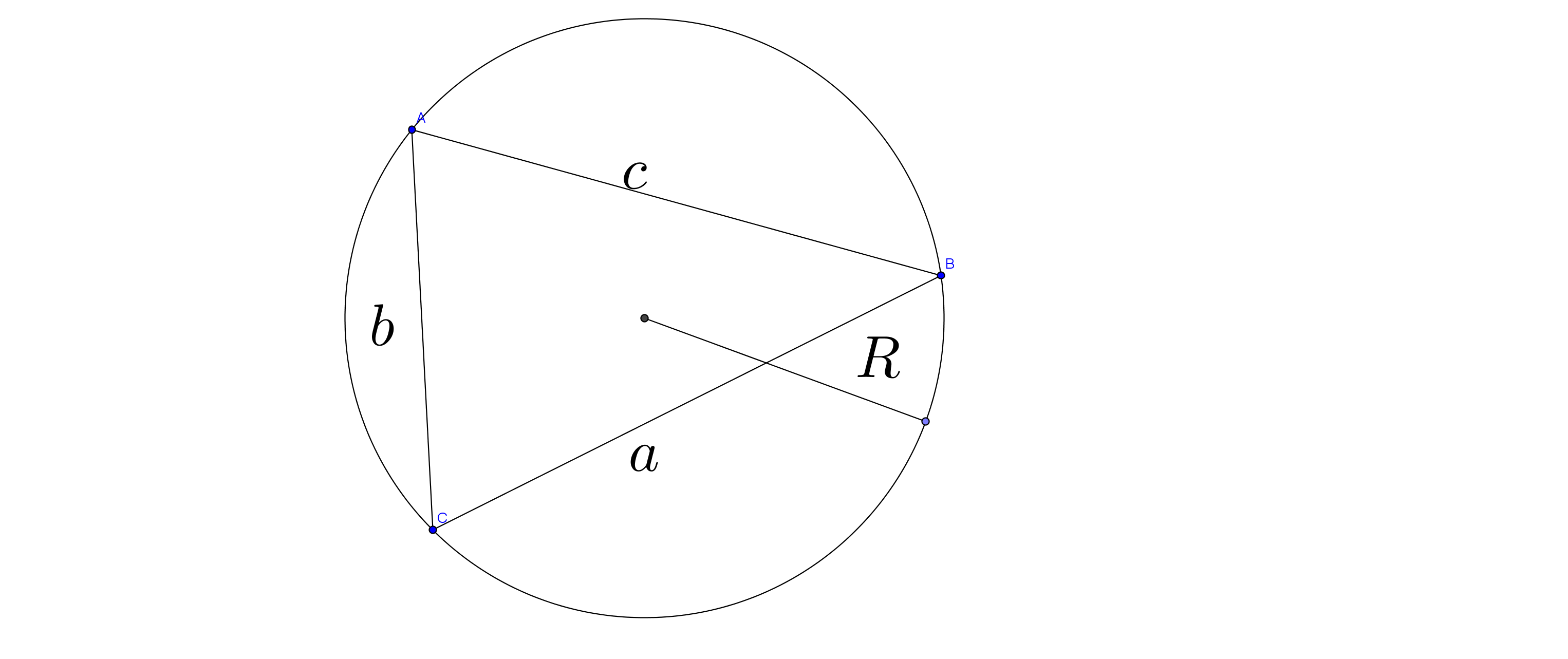
Law of Sine:

In an arbitrary triangle, there is a good property:

A larger angle corresponds to a longer side.

To prove this, an easier way can be used: Proof on Youtube

However, we can also use the law of sine.

Click to enlarge.

Click to enlarge.

When we choose another altitude, we can obtain the first part of the law of sine.

Click to enlarge.

This is the proof of the second part of law of sine using the diagram above:

And then, we can proof the proposition stated on the top of this page, since sine function is larger when the angle is larger when the angle is smaller than 90 degrees.

Even when the triangle is obtuse-angled, we can still use the formula.(for proof, the triangle drawn in the unit circle for these two cases are congruent, where the y-coordinates are the same. Or Prove By Angle Sum Formula)

Law of Cosine:

The following formula is the law of cosine, but the expression is just one part, the a, b, c can be interchanged.

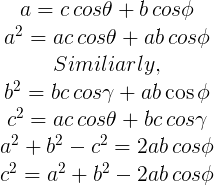
Then, we have proved the cosine law.

For more information, please read Law of Sines